During the last 60 years electricians have used offset bending tables published by Jack Benfield.  Jack Benfield was a salesman during the late 1930's who had the task of selling EMT to the electrical industry.  At that time, one reason for not accepting EMT was the difficulty with bending the tubing.  Benfield solved this problem by inventing the Benfield Bender and simplifying the mathematics of bending offsets into simple rules and tables of multipliers avoiding the use of trigonometry.  Today these tables are published in just about every handbook and manual on conduit bending and are found in the 2 million books sold as the Benfield Conduit Bending Manual.  In his book just below one of his famous Zip Guides on page 12 Jack Benfield states, "The Benfield technique works for all sizes of EMT, rigid conduit, or IMC.  The same formulas can be used with power benders on 6 inch conduit...it also works for any make of bender that may be found on any job."  The author disagrees with this statement and will tell you why in the following presentation.

The Benfield method over simplifies the bending of offsets by using approximations that have built in errors that increase with the size of pipe, the dimension of the radius, and the steepness of the bend.   In fact the author discovered that the Benfield rule of using the cosecant of the angle to multiply times the height of the offset to find the distance between bends (where his table values came from) assumes the pipe has no bends or arcs at all but follows a broken straight line path.  The Benfield shrinkage multipliers are constant when in fact the shrinkage and shrinkage multiplier are a function of the centerline bending radius. 

These errors have caused the author untold misery over the years resulting in rebending of pipe, banging the pipe on the floor to remove degrees of bend, recutting precut pipe, and sometimes discarding the offset bent pipe entirely.  It is a very frustrating task indeed to make every effort to bend an offset to 1/16 of an inch only to find that even with your utmost care in using the Benfield Tables and method that your pipe is anywhere from 3/8 to 2 inches off.  What is even more frustrating is thinking that you were the problem and not knowing that the Benfield Tables were the root cause.  After all, if these tables have been published for over 60 years and are attached to hand bender handles by manufacturers they must be correct.  However, as we shall see, this is not the case.

After developing and installing the equations found in Figures 1 and 2 in an Excel spreadsheet and a JavaScript computer program and evaluating and testing the results, they reveal that, indeed, the Benfield Tables are approximations, the best fit of the least squares or something like that.  How can a 1/2 inch bender and a 2, and 4 inch bender all have the same table when they have different bending radii?  They don't and that is why those shrinkage values always come out just a little off and become more off as the size of the raceway increases.  But with long necked connectors for EMT the errors do not cause too many problems for 1/2, 3/4, and 1 inch EMT for bends up to 30 degrees.   But if you use the Benfield Tables and technique for bends over 30 degrees or on 1 1/4 to 6 inch pipe, you are going to have trouble!

The center line bend radii for pipe sizes from 1/2 inch to 5 inches for 71 benders were entered into an Excel spread sheet and used in the calculation of shrinkage and distance between bends and this was compared to the calculated numbers using the Benfield offset formulae given on page 8  of the Benfield Conduit Bending Manual for 10 degrees, 22 1/2 degrees, 30 degrees, 45 degrees, and 60 degrees  The spreadsheet performed 3,552 calculations to reveal the following.  The errors in shrinkage for a 30 inch high offset varied from 5/16 of an inch for 1/2 inch EMT with a 22.5 degree offset to 3 1/16 inch for 5 inch rigid with a 60 degree offset.  The errors in distance between bends for a 30 inch high offset  varied from 1/16 of an inch for 1/2 inch EMT with a 30 degree offset to 4 inches for 5 inch rigid pipe with a 60 degree offset.  In 11 cases using the Benfield shrinkage values would result in precutting the pipe up to 3 1/16 inches too short.  The average error for shrinkage is 9/16 inches and the average error for distance between bends is 2 inches.  The results of these calculations and for other offset heights are so overwhelming that the author recommends using the Benfield offset formulae only for 1/2 inch to 3/4 inch EMT with bends no greater than 30 degrees.  The offset error Excel spreadsheet showing these calculations is available by clicking here.

Performing trigonometric calculations in the 1930's and until the late 1960's was a time consuming task requiring slide rules, trigonometric tables, and hand written calculations.  In the late 1960's the computer revolution began.  Today, desktop and laptop computers are found on almost every electrical job and most electricians are computer literate.  Today, Performing complex trigonometric calculations is as simple as clicking on a button in a web page.   The author has evaluated the Benfield tables and methods in order to find if computers can be used to bend more accurate offsets, and has written a web page calculator that performs mathematically correct  calculations. 

The offset calculator that uses the mathematics developed in Figures 1 and 2 is below.  There are several other offset calculators on the internet that use the Benfield Tables to  calculate shrinkage and distance between bends.  These calculators give the same errors as the original Benfield Tables and method.  If you are going to use an offset bender computer program make sure it uses the centerline bend radius and the length of the arc in the program, or better just go to http://www.electrician2.com and find the Offset Bend Calculator under the menu item "calculators."

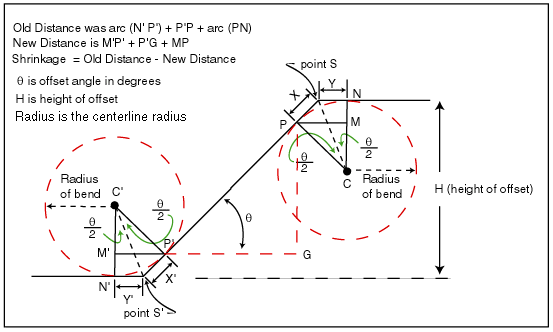
Figure 1

Figure 2

Why Use the Centerline Radius?

The reason that the centerline radius is used in the calculation is because when a pipe is bent the inside radius shortens from its original length and the outside radius lengthens from its original length, but the centerline radius stays the same length before and after bending.  In Figure 3 a blue tape was placed one foot from the end of a 3/4 EMT.  Then three wires were cut exactly one foot long.  The EMT was bent into a 90 degree bend using a hand bender.  The wires were then attached to the pipe, one at the inside radius, one at the centerline radius, and one at the outside radius.  The calculated difference between the inside radius and the outside radius is 1.45 inches.  As seen in Figure 3 that is the difference found.  However, the centerline radius did not increase or stretch in length.   Therefore the centerline arc distance represents the original length of conduit from which the arc was created.

Figure 3

Straight Pipe Length

The straight pipe length is the length of PP' in figure 1.  This length is entered in the calculator as a reference.  When the calculation is performed the calculated straight pipe length is compared to the entered value and if it is less an alert window warns the user.  Straight pipe lengths of 2 to 3 inches are recommended for small hand benders.  For larger pipes and other types of benders 1/2 the radius distance should always be a safe distance that will allow the two bends to be made.  However, this has not been verified in the field using all types of benders.  A negative straight pipe length means the two arcs are extending into each other and should be avoided.  To increase the Straight Pipe Length decrease the angle of bend.  This will also cause the distance between bends to be greater.

Straight Pipe Length = P'P in Figure 1.

Distance Between Bends

The distance between bends found by multiplying the height of the offset by the cosecant of the angle is a method given in many popular handbooks, manuals, and references. This is where the multipliers of 6 for 10 degrees, 2.6 for 22.5 degrees, 2.0 for 30 degrees, 1.4 for 45 degrees, and 1.2 for 60 degrees come from. This method is an approximation and is not mathematically correct, because it does not use the length of the arc of the bend.   For most offsets of up to 30 degrees, there is little difference in using this method or using the correct mathematical calculation. However, again for greater angles and large pipe these multipliers will give you errors that may require recutting the pipe and/or altering the bend angles. I have placed the correct calculation in the offset calculator and added a conversion for decimal to the nearest 16th of an inch in fractions.

Distance Between Bends = (angle of bend / 360) X 2 x Pi x radius + P'P as shown in Figures 1 and 2.

An illustration of using the cosecant of an angle as a multiplier when it causes a significant error can be readily understood when we consider a 90 degree offset, 90 degree being the maximum bend angle that we would probably ever use.  The cosecant of 90 degrees is 1.  Let's find the distance between bends for a 60 inch high offset using a 4 inch pipe with a 20 inch center line bend radius.  Using the cosecant the distance between bends would be the cosecant (90 degrees) x 60 or 60 inches.  If we made two 90 degree bends at 60 inches apart that should give us a 60 inch offset if the cosecant is the correct multiplier.  However, the calculator says the distance between bends should be  51 7/16 inches and the multiplier is 0.857.  Using the cosecant as a multiplier would make our offset 60 - 51 7/16 or 8 9/16 inches too high.  We would end up with a 68 9/16 inch high offset!  Why the difference?  The cosecant multiplier assumes that there are no curves or arcs in the bends and that the pipe follows a broken line path, and it would have to for two 90 degree bends 60 inches apart to give us a 60 inch height.   The calculator applies the correct math to the curves or arcs of the bends and compensates for the gain they add to the 90 degree bend or, for that matter, any bend.   If we enter a 20 inch radius and a  90 degree bend into the Developed Length Calculator we find that the gain or shrink is 8 9/16 inches.

Using the cosecant as a multiplier for angles of 10, 15, 20 and 30 degrees is a good approximation, but with computers doing the work, we can be more precise.  When you think of it, today almost every job has a desktop computer that is equivalent to what was a mainframe computer costing hundreds of thousands of dollars forty years ago.  We now have these powerful tools readily available so why not use them? 

Field Test Results:

Example 1

Here are actual test results from using the calculator and the cosecant of the angle to bend a 15 inch 90 degree offset using 3/4 inch EMT and an Ideal 3/4 inch hand bender with a 5.2 inch centerline radius (remember the cosecant of 90 degrees is 1):

	Calculator	Using the cosecant of the angle
Distance Between Bends	12 3/4 inches	15 inches inches  (1 x 15 = 15 inches)
Measured Offset Ht after bending	15 inches	17 1/2 inches
Calculated Shrinkage	10 9/16 inches	No multiplier listed (.82 by calculation)
Measured Shrinkage	10 1/2 inches	12 3/8 inches

Table 1

The calculator wins, hands down!

Although making a 90 degree offset is unusual, the calculator values can be used to make a back to back 90's or for that matter any situation where the second 90 degree bend is not in the same plane as the first 90.  Don't try this using the cosecant of 90 degrees as a multiplier!

Example 2

Here is another example using the calculator against the Zip Table values published in the Benfield Conduit Bending Manual that are shown in Table 3   A 7 inch height, 60 degree offset was made using both methods using 3/4 EMT and an Ideal 3/4 inch EMT hand bender with a 5.2 inch centerline radius.  Here is a Table of the results (remember the cosecant of 60 degrees is 1.2):

 

	Calculator	Zip Table
Distance Between Bends	7 1/2 inches	8 3/8 inches  (1.2 x 7 = 8.4 inches)
Measured Offset Ht after bending	7 inches	7 5/8 inches
Calculated Shrinkage	2 15/16 inches	3 1/2 inches (0.5 x 7 = 3 1/2)
Measured Shrinkage	2 7/8 inches	3 1/8 inches

Table 2

The results are overwhelming.  The calculator again wins hands down.

Shrink for any Bend

Shrink = 2 x radius x (tan (bend angle / 2)) - Developed Length

Developed Length is found by:

Developed Length = (angle of bend / 360) x 2 x Pi x radius

For 90 degrees the developed length is  the familiar 1.57 x radius that is derived from 90/360 x Pi x Diameter, where diameter is equal to 2 x radius.

Since the tan of 45 degrees is 1, the Shrink for a 90 degree bend is (2 x radius) - (1.57 x radius)

When Shrink is used to bend and cut pipe, one must remember that the shrink is derived using the centerline radius, not the outside radius.  Field measurements taken using the back side of a conduit can result in errors.

Here is a typical Table from a handbook from which the Table values were used:
 

Shrinkage = Shrinkage Multiplier x Offset Height

Multiplier = Cosecant of Angle

Degree of Bend in Degrees (Angle)	Multiplier	Shrinkage Multiplier in inches
10	6	1/16
15	3.9	1/8
22.5	2.6	3/16
30	2	1/4
45	1.4	3/8
60	1.2	1/2

Table 3